Random number generator enhancements for Linux 5.17 and 5.18
by Jason A. Donenfeld (zx2c4), 2022-03-18
The random number generator has undergone a few important changes for Linux 5.17 and 5.18, in an attempt to modernize both the code and the cryptography used. The smaller part of these will be released with 5.17 on Sunday, while the larger part will be merged into 5.18 on Monday, which should receive its first release candidate in a few weeks and a release in a few months.
As I wrote to Linus in the 5.18-rc1 pull request yesterday, the goal has been to shore up the RNG’s existing design with as much incremental rigor as possible, without, for now, changing anything fundamental to how the RNG behaves. It still counts entropy bits and has the same set of entropy sources as before. But, the underlying algorithms that turn those entropy sources into cryptographically secure random numbers have been overhauled. This is very much an incremental approach toward modernization. There’s a wide array of things that can be tackled in the RNG, but for the first steps, accomplished in 5.17 and 5.18, the focus has been on evolutionarily improving the existing RNG design.
Given that there have been a lot of changes during these cycles, I thought I’d step through some of the more interesting ones, some of which you may have already seen via @EdgeSecurity. In many cases, the commit messages themselves offer more detail and references than I’ll reproduce here, so I’ll include links to various commits in green. If a particular part piques your interest, or you find yourself wanting to comment on it, I would recommend clicking through to read the commit message. Of course there are also scores of other less interesting bug fixes, cleanups, nits, and such, which I won’t cover here; check the commit logs if those are your cup of tea.
As a last preliminary, if you’re more into the cryptography side of things, don’t be put off if some of the kernely concerns seem obtuse, and conversely if you’re a kernel engineer, it’s not a big deal if some of the cryptographic discussion doesn’t strike a chord; hopefully both camps will at least get something.
Mundane but essential: readability
Before talking about interesting technical changes, though, the most important improvement across 5.17 and 5.18 is that the code itself has been cleaned up, reorganized, and re-documented. I realize how incredibly mundane this is, but I cannot stress enough just how important this is. If you’re following along with this post or if you’re just generally curious about the RNG, I’d encourage you to open up random.c from the random.git tree and scroll around. Some of the below discussion relies on some familiarity with the overall design of random.c, so you may wish to refer to it. The code is divided into 6 sections, “Initialization and readiness waiting”, “Fast key erasure RNG, the ‘crng’”, “Entropy accumulation and extraction routines”, “Entropy collection routines”, “Userspace reader/writer interfaces”, and “Sysctl interface”, with only two forward declarations required, indicating a decent amount of cycle-free independence of each section.
random.c was introduced back in 1.3.30, steadily grew features, and was a pretty impressive driver for its time, but after some decades of tweaks, the general organization of the file, as well as some coding style aspects were showing some age. The documentation comments were also out of date in several places. That’s only natural for a driver this old, no matter how innovative it was. So a significant amount of work has gone into general code readability and maintainability, as well as updating the documentation. I consider these types of very unsexy improvements to be as important if not more than the various fancy modern cryptographic improvements. My hope is that this will encourage more people to read the code, find bugs, and help improve it. And it should make the task of academics studying and modeling the code a little bit easier.
Onto the technical changes.
Infrastructure and interface improvements
The most significant outward-facing change is that /dev/random and /dev/urandom are now exactly the same thing, with no differences between them at all, thanks to their unification in random: block in /dev/urandom, which was comprehensively covered by LWN. This removes a significant age-old crypto footgun, already accomplished by other operating systems eons ago. Now the only way to extract “insecure” randomness is by explicitly using getrandom(GRND_INSECURE) (which is used by, e.g., systemd for hash tables).
This is made possible thanks to a mechanism Linus added in 5.4, in random: try to actively add entropy rather than passively wait for it, in which the RNG can seed itself using cycle counter jitter in a second or so if it hasn’t already been seeded by other entropy sources, using something pretty similar to the haveged algorithm. A cycle counter is acquired using RDTSC, and a timer is armed to execute in one tick. Then schedule() is called, to force a lap through the quite complex scheduler. That timer executes at some point, with its data structures adjacent in memory to that stored cycle counter. In its execution payload, it credits one bit of entropy. That cycle counter is then dumped into the entropy input pool, a new one is acquired, and the process starts over. That’s partially voodoo, but it is what’s been there for a while.
With the “Linus Jitter Dance” having been deployed for several years now, /dev/urandom can now safely block until enough entropy is available, since we no longer risk breaking userspace by having it block indefinitely, as this self-seeding capability will unblock it decently fast. The upshot is that every Internet message board disagreement on /dev/random versus /dev/urandom has now been resolved by making everybody simultaneously right! Now, for the first time, these are both the right choice to make, in addition to getrandom(0); they all return the same bytes with the same semantics. There are only right choices.
[Update 2022-03-22: apparently we cannot yet unify /dev/random and /dev/urandom, because the day after this change made it to mainline breakage was detected on arm, m68k, microblaze, sparc32, and xtensa, and Linus decided to revert with Revert “random: block in /dev/urandom”. Sometimes that’s just how it goes, and now we’ll need to regroup and see if there are other ways of solving this problem down the road. For now we fallback to attempting the same thing opportunistically with random: opportunistically initialize on /dev/urandom reads, which means we should accomplish mostly the same thing on platforms with fast cycle counters, such as x86.]
While that solves issues related to having good randomness at boot time, we now also handle maintaining good randomness when a virtual machine forks or clones, with random: add mechanism for VM forks to reinitialize crng. Suppose you take a snapshot of a VM, duplicate it, and then start those two VMs from the same snapshot. Their initial entropy pools will contain exactly the same data, and the key used to generate random numbers will be the same. Therefore, both VMs will generate the same random numbers, which is a pretty egregious violation of what we all expect from a good RNG. The above API into the RNG is used by a new driver I wrote for the virtual “vmgenid” hardware device, supported by QEMU, Hyper-V, and VMware, in virt: vmgenid: notify RNG of VM fork and supply generation ID. This hypervisor-assisted mechanism allows the kernel to be notified when a VM is forked, alongside a unique ID that is hashed into the RNG’s entropy pool. This too was covered in depth by LWN.
That notification is slightly racy, by design unfortunately, but the virtual hardware only exposes a 16-byte blob, which is a bit too cumbersome to poll. It would be nice if future virtual hardware additionally exposes a 32-bit word-sized counter, which can be polled as a simple memory-mapped word. Either way, though, the race window is exceedingly small, and moving from 5 minutes of problems to some microseconds is doubtlessly a significant improvement.
The first in-kernel user of this functionality is naturally WireGuard, which makes use of it with wireguard: device: clear keys on VM fork. This commit prevents erroneously encrypting different plaintext with the same key and nonce combination, which is generally considered to be a cryptographically catastrophic event. Here it is in action, where you can see me saving and restoring the WireGuard test suite VM with QEMU’s monitor:
I expect future kernels to make use of this functionality in other drivers that are sensitive to nonce reuse, and discussions are already underway for exposing this event to userspace as well.
Addressing a relatedly quiescent circumstance, a CPU hotplug handler added in random: clear fast pool, crng, and batches in cpuhp bring up ensures that CPUs coming online don’t accidentally serve stale batches of random bytes. This was part of more general work to make the RNG more PREEMPT_RT-friendly, by avoiding spinlocks in the interrupt handler, moving to a deferred mechanism instead in random: defer fast pool mixing to worker, and by avoiding spinlocks in batched randomness by making use of a local lock, with random: remove batched entropy locking.
Cryptographic improvements
In 5.17, I began by swapping out SHA-1 for BLAKE2s with random: use BLAKE2s instead of SHA1 in extraction. With SHA-1 having been broken quite mercilessly, this was an easy change to make. Crypto-wise, that change allowed us to improve the forward security of the entropy input pool from 80 bits to 128 bits, as well as providing a documented way of mixing in RDRAND input (via BLAKE2s’s salt and personal fields) rather than the eyebrow-raising abuse of SHA-1’s initialization constants used before. While the particular usage of SHA-1 prior wasn’t horrible, it wasn’t especially great either, and switching to BLAKE2s set the stage for us to be able to do more interesting things with hashing and keyed hashing for 5.18 to further improve security. It also offers modest performance improvements.
So first on the plate for 5.18 is random: use computational hash for entropy extraction, in which the old entropy pool, based on a 4096-bit LFSR, is replaced with — you guessed it — BLAKE2s.
The old LFSR used for entropy collection had a few desirable attributes for the context in which it was created. For example, the state was huge, which meant that /dev/random would be able to output quite a bit of accumulated entropy before blocking, back in the days of yore when /dev/random blocked. It was also, in its time, quite fast at accumulating entropy byte-by-byte. And its diffusion was relatively high, which meant that changes would ripple across several words of state quickly.
However, it also suffered from a few related quasi-vulnerabilities. Because an LFSR is linear, inputs learned by an attacker can be undone, but moreover, if the state of the pool leaks, its contents can be controlled and even entirely zeroed out. I had Boolector solve this SMT2 script in a few seconds on my laptop, resulting in a silly proof of concept C demonstrator, and one could pretty easily do even more interesting things by coding this up in a computer algebra system like Sage or Magma instead. For basically all recent formal models of RNGs, these sorts of attacks represent a significant cryptographic flaw. But how does this manifest practically? If an attacker has access to the system to such a degree that he can learn the internal state of the RNG, arguably there are other lower hanging vulnerabilities — side-channel, infoleak, or otherwise — that might have higher priority. On the other hand, seed files are frequently used on systems that have a hard time generating much entropy on their own, and these seed files, being files, often leak or are duplicated and distributed accidentally, or are even seeded over the Internet intentionally, where their contents might be recorded or tampered with. Seen this way, an otherwise quasi-implausible vulnerability might be worth caring about at least a little bit.
A few candidates were considered for replacing the LFSR-based entropy pool. Dodis 2013 suggests universal hashing with a secret seed, which is pretty fast, but the requirement for a secret seed proved problematic: how do we generate a random secret in the first place? A few years later, Dodis 2019 explored the use of cryptographic hash functions as seedless entropy extractors. That paper suggests various constructions and proofs that are practically applicable.
So we were able to replace the LFSR in mix_pool_bytes() with a simple call to blake2s_update(). Extracting from the pool then becomes a simple matter of calling blake2s_final() and doing a small HKDF-like or BLAKE2X-like expansion, using 256 bits of RDSEED, RDRAND, or RDTSC (depending on CPU capabilities) as a salt like the prior design. One output reinitializes the pool for forward secrecy by making it the “key” in a fresh keyed BLAKE2s instance, while the other becomes the new seed for the ChaCha-based pseudorandom number generator (the “crng”). Written out, seed extraction looks like this:
τ = blake2s(key=last_key, entropy₁ ‖ entropy₂ ‖ … ‖ entropyₙ)
κ₁ = blake2s(key=τ, RDSEED ‖ 0x0)
κ₂ = blake2s(key=τ, RDSEED ‖ 0x1)
last_key = κ₁
crng_seed = κ₂
Going with a cryptographic hash function then made it possible to replace the complicated entropy accounting we had before with just a linear counter, in random: use linear min-entropy accumulation crediting. The above paper moves us into the random oracle model, where we can consider min-entropy accumulation to be essentially linear, which simplified quite a bit of code. At the same time, we increased the threshold for RNG initialization from 128 bits to 256 bits of collected entropy, which might make the RNG more suitable for generating certain types of secret keys (though as we’ll discuss later, the entropy crediting system is not very meaningful in itself). This computational hash approach wound up offering some significant performance improvements over the LFSR as well.
In a similar vein, the interrupt entropy accumulator has been reworked in random: use SipHash as interrupt entropy accumulator. All ordinary entropy sources feed data into the aforementioned mix_pool_bytes(), which now uses the cryptographic hash function BLAKE2s. The interrupt handler, however, does not have the CPU budget available to call into either a fully-fledged hash function or the LFSR that preceded it. For that reason, the RNG has the fast_mix() function, which is supposed to be a lighter-weight accumulator, originally contributed by anonymous contributor extraordinaire George Spelvin. Unfortunately, the custom add-rotate-xor permutation contributed by George is really very weak on several fronts (for example, xoring new inputs directly into the entire state), with unclear cryptographic design goals. Fortunately, one round of SipHash on 64-bit or HalfSipHash on 32-bit fits in around the same CPU budget, so fast_mix() now does word-at-a-time SipHash-1-x/HalfSipHash-1-x.
The choice to go with a round of SipHash per word seems like a simple and easy one, now that we’ve arrived at it. It was not easy to arrive there, however. The interrupt entropy accumulator assumes that inputs are generally not malicious. For the most part they aren’t — a cycle counter, a jiffies read, and a fixed return address are all somewhat difficult to massage into a real-world attack. On the other hand, we also currently mix in the value of an interrupt handler register chosen by round-robin, which could be more fruitful to an attacker. Nonetheless, we don’t currently have the CPU budget to assume malicious inputs, so we keep the same security model as prior, and perhaps this is something we can revisit in the future with new crypto, simpler inputs, or fancy ring buffers. Anyway, assuming inputs are non-malicious, we have some interesting choices for entropy accumulators.
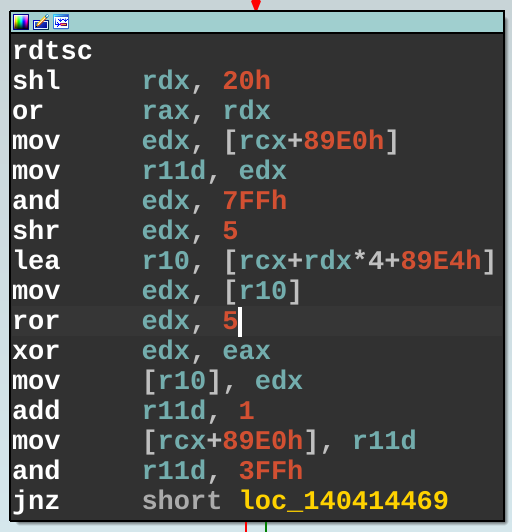
If we’re able to assume the inputs fit a 2-monotone distribution, we can get away with a very fast rotate-xor construction, which is what the NT kernel uses. This would take the form of x = ror64(x, 19) ^ input or x = ror32(x, 7) ^ input, which is doubtlessly very fast to compute. NT actually uses the less optimal rotation constant 5, which you can tease out of various functions such as ntoskrnl.exe!KiInterruptSubDispatch:
Unfortunately, while the timestamps are 2-monotone, the register values and return addresses are not. So until we simplify what we collect during each interrupt, that’s a bit of a non-starter.
On the other hand, if we’re able to assume that the inputs are independent and identically distributed (IID), we can simply pick a max-period linear function with no non-trivial invariant subspace, and use it in the form of x = f(x) ^ input. And while this was initially quite attractive — it implies just making a super fast max-period LFSR — the IID requirement also quite clearly does not apply to our input data.
So, finally, we return to the paper mentioned earlier that shows hash functions make good entropy accumulators (“condensers” in the literature), and observe that pseudorandom function instances can approximately behave like random oracles, provided that the key is uniformly random. But since we’re not concerned with malicious inputs (remember our interrupt security model), we can pick a fixed SipHash key, which is not secret, knowing that “nature” won’t interact with a sufficiently chosen fixed key by accident. Then, after each run of 64 interrupts or 1 second, we dump the accumulated SipHash state into mix_pool_bytes(), as before, which does use a proper hash function. Taken together, on 64-bit platforms this amounts to the following. At boot time, per CPU:
siphash_state_t irq_state = siphash_init(key={0, 0, 0, 0});
Then on each interrupt, data accumulates into that state:
u64 inputs[] = {
rdtsc ^ rol64(jiffies, 32) ^ irq,
ret address
};
siphash_update(irq_state, inputs);
Note that the input data collected there and xored together like that is unchanged from earlier releases, and something that might be revisited for future ones (though in this release I did clean up the code for it in random: deobfuscate irq u32/u64 contributions). Finally, after 64 interrupts (or less if a second has elapsed), running in a deferred non-interrupt worker:
blake2s_update(input_pool, irq_state, sizeof(irq_state) / 2);
When revisiting entropy input data heuristics in future releases, this may well change and improve yet again, but for now, the new SipHash-based fast_mix() is strictly better than what it replaces.
I touched on RDSEED usage earlier, and there are in fact some more detailed changes on that topic. In random: use RDSEED instead of RDRAND in entropy extraction, the RNG now uses RDSEED, if available, before falling back to RDRAND and eventually RDTSC. Since the CPU’s RNG is just another entropy input source — one we happen to call at boot time for initial seeding and during each subsequent reseeding — we might as well use its best source. We’re not using it as part of the direct generation of random numbers itself, but just as an additional entropy input, and hence there’s not a need for the speed improvements of RDRAND over RDSEED. (Incidentally I recently removed direct RDRAND-usage from systemd too.)
This notion of treating RDSEED as just another entropy input was enforced in a few additional commits, random: ensure early RDSEED goes through mixer on init and after. Prior, RDRAND would be xor’d into various inputs and outputs, sort of haphazardly. This is no more. Now, RDSEED goes into the cryptographically secure hash function that comprises our entropy pool. That means tinfoil hatters who are concerned about ridiculous hypothetical CPU backdoors have one less concern to worry about, since such a backdoor would now require a hash pre-image, which is considered to be computationally infeasible for BLAKE2s. Of course RDSEED could still return a knowable-in-advance sequence, and for that reason CONFIG_RANDOM_TRUST_CPU still exists for whether or not the entropy pool is credited for RDSEED input. But now, for people who have CONFIG_RANDOM_TRUST_CPU=n, you can perhaps rest easier knowing that RDRAND isn’t being combined insecurely with other entropy, potentially tainting it, the way it was before. Forcing RDSEED through the hash function means it always only ever contributes or does nothing, but never hurts. More importantly, it makes modeling our entropy inputs a lot simpler, since now they all converge to the same path.
Continuing the theme of doing things in only one way: in the past, entropy has been ingested a bit differently during early boot. The first 64 bytes of entropy either would get directly xor’d into the ChaCha key we use for generating random bytes, or would be mixed with the key via yet-another LFSR. Neither one of these mechanisms is terrific for a variety of reasons. Instead, we first replaced the LFSR with our cryptographically secure hash function in random: use hash function for crng_slow_load(), and later after the aforementioned deferred interrupt mixing improvements, replaced the direct-xor method with that same hash function, in random: do crng pre-init loading in worker rather than irq.
Finally, the “crng” is our ChaCha-based pseudorandom number generator, which takes a 32-byte “seed” as a ChaCha key, and then expands this indefinitely, so that users of the RNG can have an unlimited stream of random numbers. The seed comes from the various entropy sources that pass through BLAKE2s. An important property of the crng is that if the kernel is compromised (by, say, a Heartbleed-like vulnerability), it should not be possible to go back in time and learn which random numbers were generated previously, a type of forward security. The crng accomplishes this with Dan Bernstein’s fast key erasure RNG proposal. The prior implementation of this handled the ChaCha block counter in a somewhat precarious way, and had complex logic for handling NUMA nodes that led to numerous bugs. In random: use simpler fast key erasure flow on per-cpu keys, we return to a design much closer to Bernstein’s original proposal, except that we extend it to operate on per-cpu keys.
Fast key erasure is a simple idea: expand a stream cipher, such as ChaCha or AES-CTR, to generate some random bytes. When you’re done generating those bytes, use the first few to overwrite the key used by that stream cipher, to have forward security, and return the rest to the caller. In the per-cpu extension of that design, all entropy is extracted to a “base” crng. Then, each time a per-cpu crng is used, it makes sure that it is up to date with the latest entropy in the base crng. If it is, then it continues on doing fast key erasure with its own key. If it isn’t, then it does fast key erasure with the base crng’s key in order to derive its new one. Borrowing a diagram from the commit message, this looks like:
If you’re looking for a simpler example of non-per-cpu fast key erasure, I also recently implemented it using AES for Go’s Plan 9 crypto/rand package. And SUPERCOP has a delightfully trivial implementation.
A huge advantage of the per-cpu approach is that the crng doesn’t need any locking in the fast path; it simply needs to disable preemption (via a local lock) when doing fast key erasure on its key. The first ChaCha block generated is used for both the new key and for the first 32 bytes of random output for the caller. When that block is done, preemption can be re-enabled, and subsequent ChaCha blocks can be computed on entirely stack-local data, which means no locking or preemption-toggling of any sort. An Intel test robot apparently noticed an 8450% performance improvement in multicore scenarios, as you might expect. And in contrast to the old design, that fast key erasure stage happens immediately, with the first block, rather than after the entire operation is done and locks have been dropped, which gives us a lot stronger assurances about it.
Additionally, the base crng is now reseeded a bit more often during early boot. In random: reseed more often immediately after booting, rather than reseeding every 5 minutes, as before, we now start out reseeding at a minimum mark of 5 seconds, and then double that until we hit 5 minutes, after which we resume the ordinary schedule. The idea is that at boot, we’re getting entropy from various places, and we’re not very sure which of early boot entropy is good and which isn’t. Even when we’re crediting the entropy, we’re still not totally certain that it’s any good. Since boot is the one time (aside from a compromise) that we have zero entropy, it’s important that we shepherd entropy into the crng fairly often. And if you’re a skeptic of the aforementioned Linus Jitter Dance, this means that you’ll likely receive another infusion of entropy pretty soon after.
Moving forward
The above are some of the highlights in the process of modernizing the RNG’s current design. In the future, however, it may be prudent to start revisiting some of the original design decisions and questions of entropy collection.
For example, the current entropy crediting mechanism isn’t an entirely robust way of preventing the “premature next” problem, whereby the crng is reseeded too early, allowing an attacker who has previously compromised the pool to bruteforce new inputs that are added to it. We enforce 256 bits of entropy “credits” before we’ll allow reseeding, and as mentioned, reseeding usually only happens once every 5 minutes, so for the most part we avoid prematurely reseeding the crng. However, since we just keep track of a single counter, a single malicious entropy source could be responsible for all of the credits except for the one or two or forty or so that an attacker would then bruteforce. Typical solutions to this usually involve something like the “Fortuna” scheduler, used in a variety of other operating systems, or more generally, using multiple input buckets, and some type of scheduling system — round-robin or secret-key based or otherwise — to decide how to distribute entropy and the rate at which the buckets are used. There are interesting and non-obvious choices to make there as well. Whether or not that approach will prove appealing remains to be seen. There may be a trade-off to consider between system complexity and which attacks are worth defending against.
Similarly, we may in the future revisit the wisdom of the entropy estimation mechanism, which arguably introduces a side channel. The general concept of entropy estimation to begin with is probably impossible to do robustly. For that reason, for most entropy sources, we either credit 1 bit or 0 bits, depending on some hard-coded decision on whether the source can be trusted to not be terrible. By choosing a maximum of 1 bit for those sources, we’re really just saying, “this is a contributory event” or not, and hopefully those decisions are sufficiently conservative. However, we currently treat input devices (such as mouses and keyboards) and rotational disk drives as contributing a variable amount of entropy, which we “estimate” by looking at the difference in timing between events, and the difference in differences, and the difference in difference in differences. (For those following along with the C, take a look at add_timer_randomness().) The amount of total entropy we’ve collected is exposed to userspace in the /proc/sys/kernel/random/entropy_avail file, or when getrandom(0) unblocks for the first time. Since that estimation is making a judgment about a piece of data that is being added to the pool (the timestamp), and that estimation also influences a public piece of information (entropy_avail), the estimation process leaks some amount of data to the public. This might be rather theoretical, but it’s certainly not pretty either. An immediate solution might be to just treat those sources as contributing 1 bit, always, like we do other types of sources. But it’s also worth noting that using a scheduler, as discussed above, would eliminate the need in the first place for any type of entropy estimation or accounting.
On the topic of entropy collection heuristics in general, there are a dozen miniature projects and avenues of research to be done, in terms of what we collect on each potentially entropic event and how we collect it. One such mini-project: right now most sources also mix in RDTSC and a jiffies value. Is that ideal? Is there something better? Sounds like a worthwhile investigation, and there are many similar ones like it, for which I’d be happy to hear ideas and see patches.
As each component’s design is updated, I also hope to spend a bit of time working with academia on formal analysis. While there’s been a bit of “theory skepticism” on LKML before, I still think there’s great value in being able to reason robustly about what we’re doing in the RNG, and already engaging with the literature has been a useful guide.
The changes in 5.17 and 5.18 were quite numerous (in commit count, at least) because so much of the necessary cleanup and modernization work was low-hanging and, indeed, necessary. Though low hanging, each part did require a decent amount of analysis and care. But it still was fundamentally part of a modernization project that intentionally kept much of the original core design intact, because generally kernel development prefers incremental changes over radical ones. Moving forward, in order to re-examine some of those original design decisions, I expect the pace to actually slow down a bit. Either way, I think the changes of these last two cycles have successfully catapulted our RNG into 2022, and we now have a firm foundation upon which to make future improvements.
Lastly, there’s still a number of months before 5.18 comes out, during which time I’ll be sending periodic bug-fix patchsets. So if you’ve been following along here carefully and notice an issue, please don’t hesitate to send me an email.